Princeton University
The Interdisciplinary Doctoral Program in the Humanities
HUM 598, M-u-l-t-i-p-l-i-c-i-t-y
Philip Ording & David Reinfurt
Mondays, 1:30–4:20 pm
Spring 2021
In this course, students explore graphic design from the vantage point of topology and topology through the practice of graphic design. We investigate topology at the junctions of surface, network, and set, illustrating the schematic nature of these configurations, as they appear in the context of certain problems in modern and contemporary graphic design. Such as, how to render figures that take multiple forms? Student design work and topological experiments are guided through class prompts, readings, and discussion. No particular experience in design or mathematics required.
Print syllabus / Download readings
 
Around 1736, Swiss mathematician Leonhard Euler described a geometry of connections in a paper of numbered assertions. The first goes like this:
1. THE branch of geometry that deals with magnitudes has been zealously studied throughout the past, but there is another branch that has been almost unknown up to now; Leibnitz spoke of it first, calling it the “geometry of position” (geometria situs). This branch of geometry deals with relations dependent on position alone, and investigates the properties of position; it does not take magnitudes into consideration, nor does it involve calculation with quantities. But as yet no satisfactory definition has been given of the problems that belong to this geometry of position or of the method to be used in solving them. Recently there was announced a problem that, while it certainly seemed to belong to geometry, was nevertheless so designed that it did not call for the determination of a magnitude, nor could it be solved by quantitative calculation; consequently I did not hesitate to assign it to the geometry of position, especially since the solution required only the consideration of position, calculation being of no use. In this paper I shall give an account of the method that I discovered for solving this type of problem, which may serve as an example of the geometry of position.
225 years later, designers Ray and Charles Eames unpacked this "geometry of connections," or topology, in their first exhibition designed and produced to inaugurate the California Museum of Science and Industry. “Mathematica” was an exhibition about mathematics for a mass and diverse audience. It was originated by the Eames Office following an invitation to propose an appropriate exhibition for the new museum. 
Ray [↑] described what they meant to do in an interview with the Library of Congress from 1980:
Yes. The whole purpose of that show was "Lifting the corner of the tent" to let people know the pleasure and the joy that mathematicians had in their work. So when you see the workings of any of those things — the soap bubble — it reflects the terrific joy that was originally felt in the discovery of that model, or in the use of models, the use of thinking, and the result of observation and relationships in observation, and relationships of knowing what someone did and someone didn't do. The chart shows how different people were influenced by different things, things happening because of other things, as a result of other things happening, things in the past happening, things coming together at the right time — all those layers of happenings. 
Mathematica used hands-on mathematical models, extensive graphics, visual demonstrations, and even a collection of two-minute films designed for one viewer at a time, to address a collection of areas of contemporary mathematics. One of these was topology.
Returning to Euler, the second paragraph lays out his particular problem:
2. The problem, which I understand is quite well known, is stated as follows: In the town of Königsberg in Prussia there is an island A, called “Kneiphof,” with the two branches of the river (Pregel) flowing around it, as shown in Figure 1. There are seven bridges, a, b, c, d, e, f and g, crossing the two branches. The question is whether a person can plan a walk in such a way that he will cross each of these bridges once but not more than once. I was told that while some denied the possibility of doing this and others were in doubt, there were none who maintained that it was actually possible. On the basis of the above I formulated the following very general problem for myself: Given any configuration of the river and the branches into which it may divide, as well as any number of bridges, to determine whether or not it is possible to cross each bridge exactly once.
Schematically, the setup looks like this:

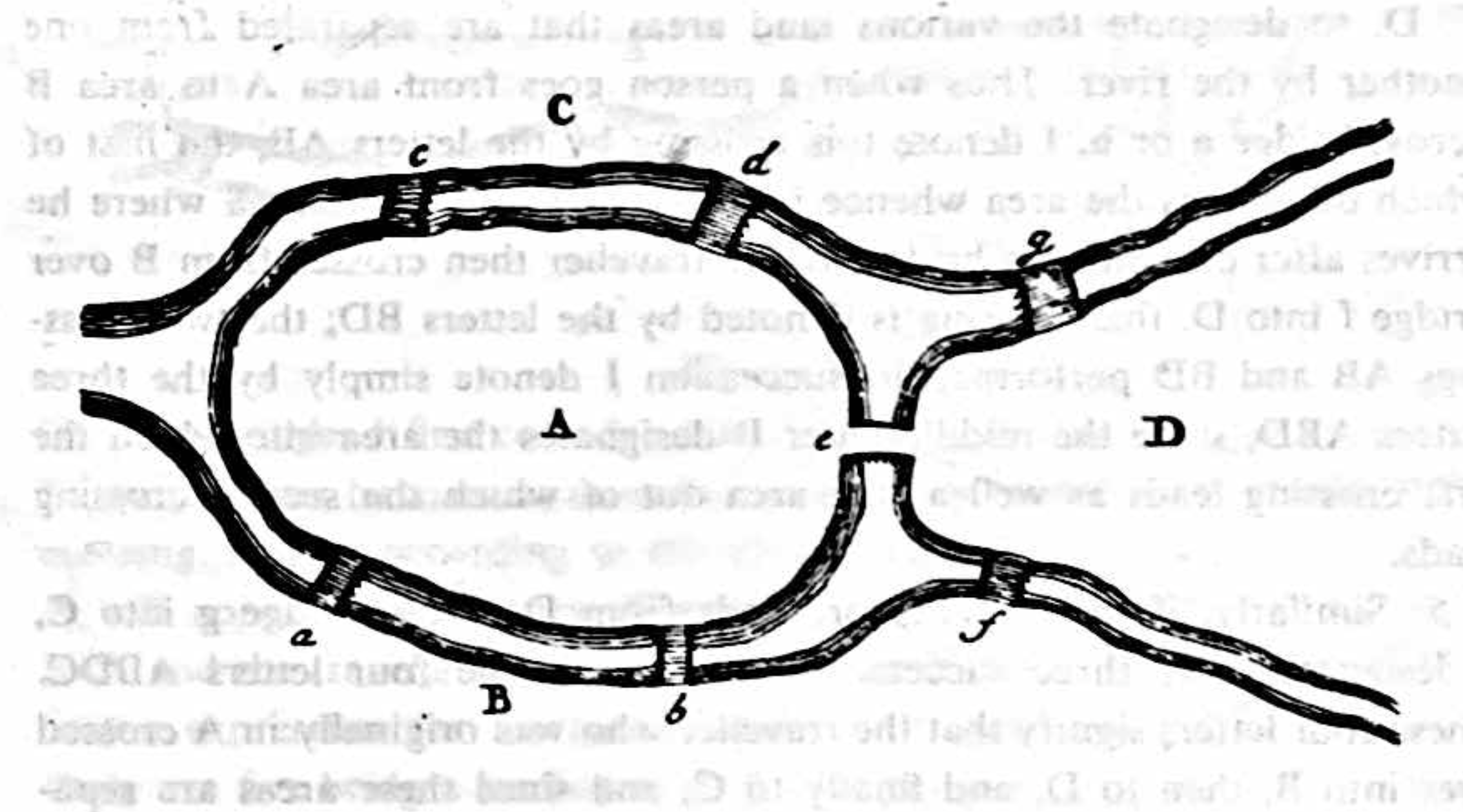
The Seven Bridges of Königsberg is a widely known problem in mathematics and foundational for Topology. Meanwhile in the intervening years, what was Königsberg is now Kaliningrad; two bridges were bombed in World War II (later rebuilt); and two more were removed to make room for a highway. The Seven Bridges of Königsberg are now The Five Bridges of Kaliningrad.
This will be a class about how things change and what stays the same when they do. It will be a class about the overlaps between two (perhaps) seemingly divergent fields, Topology and Graphic Design. We will look at one from the point of view of the other and hopefully we will discover what Graphic Design might offer to Topology, and conversely, why Topology may be important to Graphic Design, particularly now. 
We will look at bridges, knots, dancers, snowflakes, inside-out spheres, fonts, space-filling curves, maps, string figures, and multi-character storylines, and we will ask in each case, given the multiple examples, what do they have in common? What does *not* change? Exactly how are they fundamentally connected? The Eames' meta-thesis on design, repeated in numerous forms over the years, will be good to keep in mind:
Eventually everything connects — people, ideas, objects ... the quality of the connections is the key to quality per se.
February 8, 2021
The problem of multiplicity

Readings
Multiplicity.pdf (Italo Calvino)
The-Garden-of-Forking-Paths.pdf (Jorge Luis Borges)

Resources
Locus Solo (Trisha Brown)
“Most of what science orders,” Phylis and Philip Morrison remind us, “was once unknown and was newly grasped while it remained in a more or less extended period of doubt and uncertainty.” The geometry of position remained in such a period of novelty for at least a century after Euler solved the bridges problem. Topology in the mid 1800s was a collection of examples and counterexamples at the periphery of mathematics. A decisive step forward was made by the German mathematician Bernhard Riemann in his 1854 lecture "On the Hypotheses Which Lie at the Foundations of Geometry" in which he outlined the notion of a topological manifold. He begins by noting that: 
few and far between are the occasions for forming notions whose specialisations make up a continuous manifoldness, that the only simple notions whose specialisations form a multiply extended manifoldness are the positions of perceived objects and colours.
The awkward language of “specialisations” and “manifoldness” is due in part to the avant garde nature of Riemann’s project. He wants to identify spatial features that are pre-geometric, which means that familiar spatial terms of magnitude and measure are prohibited. Euler confronted the same issue. But unlike the 1-dimensional bridges of Königsberg, the problem Riemann set himself was to construct a metaspace with 1, 2, 3, or any number of dimensions. Riemann proceeds step by step: For a 1-dimensional manifold,
the true character is that in it a continuous progress from a point is possible only on two sides, forwards or backwards.
He mentioned color already, to which we can add the spectrum of sound. Consider for example the bow position as you listen to songs for the tape-bow violin by Laurie Anderson.

On to the next dimension... Riemann continues:
If one now supposes that this manifoldness in its turn passes over into another entirely different, and again in a definite way, namely so that each point passes over into a definite point of the other, then all the specialisations so obtained form a doubly extended manifoldness.
To get past the linguistic hurdles of this passage, let's extend the musical analogy. Think of a 1-manifold as a tune that begins on a particular note. A slightly different tune will result if it is shifted up or down in pitch. The space formed by transposing the tune arbitrarily in pitch forms a 2-manifold. Two dimensions of music are especially visible in a player piano scroll like the one below, Study for Piano Player No. 36 by Conlon Nancarrow.

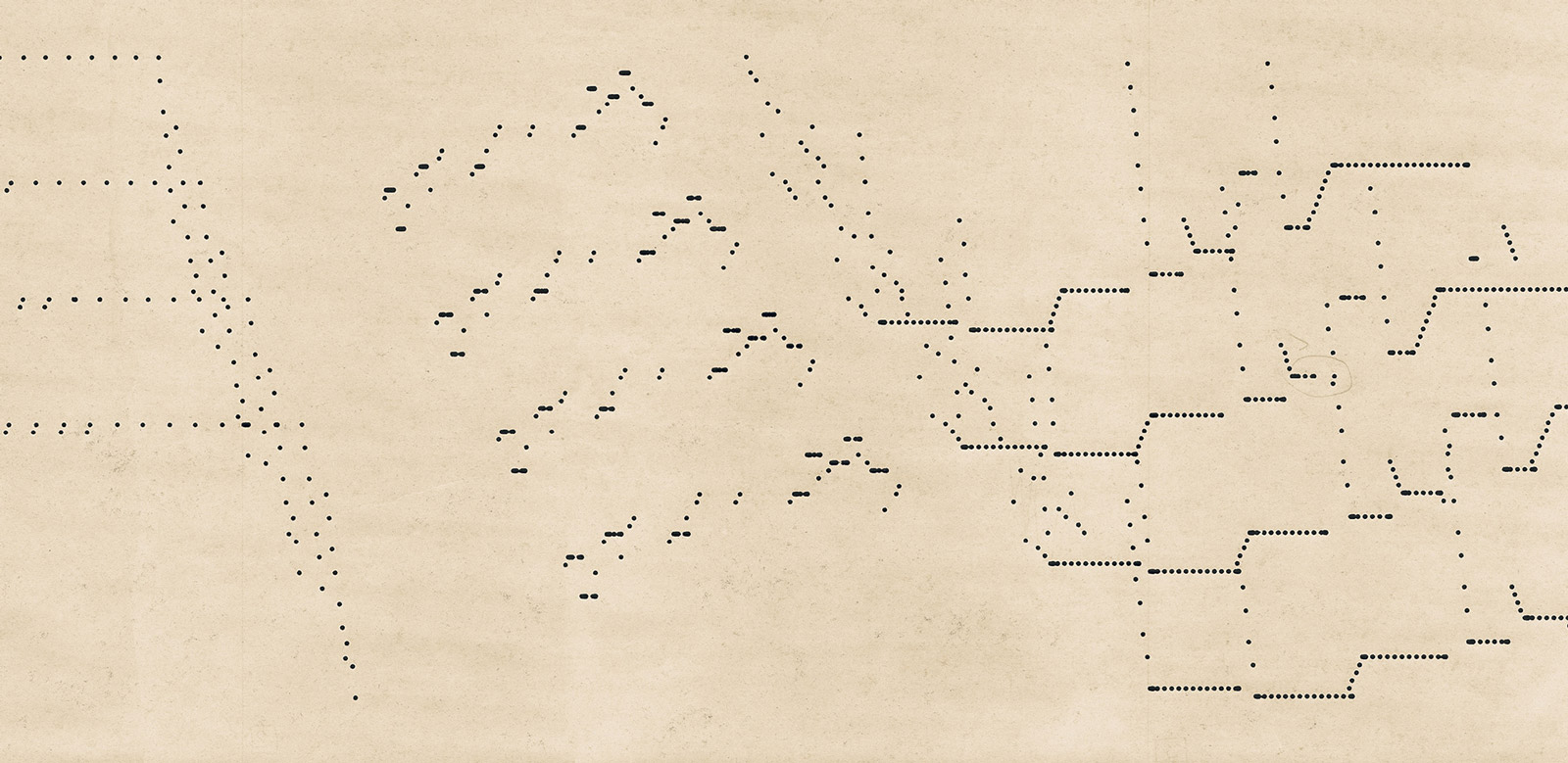
The 3- and higher-dimensional manifolds are constructed by analogy:
In a similar manner one obtains a triply extended manifoldness, if one imagines a doubly extended one passing over in a definite way to another entirely different; and it is easy to see how this construction may be continued.
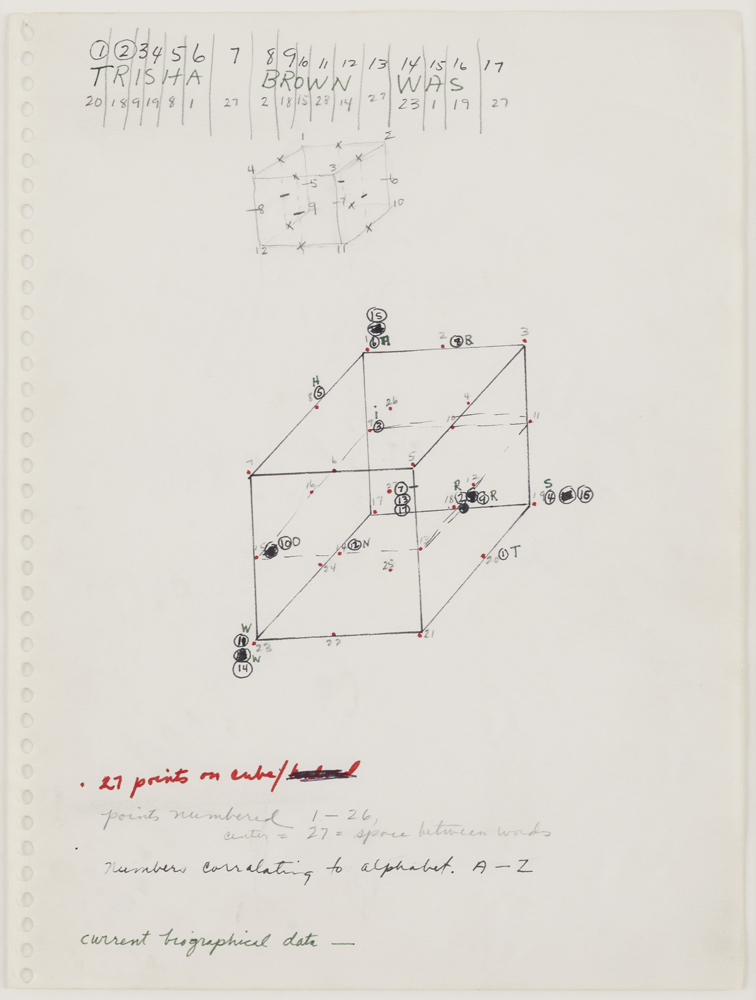
These manifolds are more difficult to visualize than 1-manifolds (curves) and 2-manifolds (surfaces). For an example of a discrete 3-manifold, watch Locus Solo, the dance Trisha Brown devised from a cubical framework. Each of 26 points on the surface of the cube corresponds to a different letter of the alphabet. In a reversal of Euler’s method, the series of letters in a given text dictate the dancer’s path. 

Before giving the above construction, Riemann apologized to his audience for not being “practised in such undertakings of a philosophical nature where the difficulty lies more in the notions themselves than in the construction.” Rather than attempt such an undertaking ourselves here, we wish to lean on the philosophico-literary observations of Six Memos for the Next Millenium by Italian writer Italo Calvino. The memos are lectures he was invited to give as Charles Eliot Norton Professor of Poetry at Harvard University. Each lecture is organized around a one-word literary value. The fifth lecture Calvino drafted was on "Multiplicity." About three quarters of the way through, Calvino gets down to business:
It is time to put a little order into the suggestions I have put forward as examples of multiplicity. There is such a thing as the unified text that is written as the expression of a single voice, but that reveals itself as open to interpretation on several levels. Here the prize for an inventive tour-de-force goes to Alfred Jarry for L'amour absolu (1899), a fifty-page novel that can be read as three completely different stories: (1) the vigil of a condemned man in his cell the night before his execution; (2) the monologue of a man suffering from insomnia, who when half asleep dreams that he has been condemned to death; (3) the story of Christ. Then there is the manifold text, which replaces the oneness of a thinking “I” with a multiplicity of subjects, voices, and views of the world, on the model of what Mikhail Bakhtin has called “dialogic” or “polyphonic” or “carnivalesque,” tracing its antecedents from Plato through Rabelais to Dostoevsky. There is the type of work that, in the attempt to contain everything possible, does not manage to take on a form, to create outlines for itself, and so remains incomplete by its very nature, as we saw in the cases of Gadda and Musil.
As a short example of the last type, he cites "The Garden of Forking Paths," one of the short stories in the collection Labyrinths by the Argentine poet, essayist, and author Jorge Luis Borges. 

Calvino picks the thought back up several pages later:
I have come to the end of this apologia for the novel as a vast net. Someone might object that the more the work tends toward the multiplication of possibilities, the further it departs from that unicum which is the self of the writer, his inner sincerity and the discovery of his own truth. But I would answer: Who are we, who is each one of us, if not a combinatoria of experiences, information, books we have read, things imagined? Each life is an encyclopedia, a library, an inventory of objects, a series of styles, and everything can be constantly shuffled and reordered in every way conceivable.
But perhaps the answer that stands closest to my heart is something else: Think what it would be to have a work conceived from outside the self; a work that would let us escape the limited perspective of the individual ego, not only to enter into selves like our own but to give speech to that which has no language, to the bird perching on the edge of the gutter, to the tree in spring and the tree in fall, to stone, to cement, to plastic. . . . .
Was this not perhaps what Ovid was aiming at, when he wrote about the continuity of forms? And what Lucretius was aiming at when he identified himself with that nature common to each and every thing?
February 15, 2021
The meta problem

Readings
Letter-&-Spirit.pdf (Dexter Sinister)
In the early 1980s, on the pages of academic design journal Visible Language, a classic thesis-antithesis-synthesis played out around the technological and philosophical fine points of computer-assisted type design. Stanford professor Donald Knuth begins with his article, “The Concept of a Meta-font” (Winter 1981). Two years prior, Knuth had conceived and programmed MetaFont — a software that enabled users to generate unlimited numbers of fonts by controlling a limited set of parameters.

The article is a performative account of his intervening attempts, using MetaFont to harness the essential “intelligence” of letterforms. In Knuth’s view, the way a single letter is drawn—an a priori A, say—presupposes and informs all other letters in the same font. This information can be isolated, turned into a set of instructions, and put to work computer-auto- mating the generation of new characters by filling in the features between two or more variables such as weight or slant.
Such intelligence is (and has always been) implicit in any typeface, but Knuth is out to omit all ambiguity and install a more definite system. He acknowledges that this preoccupation with designing meta-level instructions rather than the fonts themselves is typical of the contemporary inclination to view things “from the outside, at a more abstract level, with what we feel is a more mature understanding.” From this elevated vantage, MetaFont was set up to oversee 
how the letters would change in different circumstances.
A year later, fellow mathematician Douglas Hofstadter responded with his “MetaFont, Metamathematics, and Metaphysics” (Autumn 1982). While “charmed” by Knuth’s thesis, and admitting the bias of his own interests in artificial intelligence and aesthetic theory, Hofstadter proceeds to shoot down his colleague’s apparent claim that the shape of any given letterform is “mathematically containable.”To support his case, he invokes mathematician Kurt Gödel’s Incompleteness Theorems, which assert that any account of a logically coherent system always contains one root-level instance that cannot itself be contained by that account. Hofstadter’s antithesis then usefully couches the debate in terms of “the letter of the law” versus “the spirit of the law,” a familiar antinomy that posits an absolute deference to a set of set rules against a consistent-yet-fluid set of principles. Our prevailing legal system is, of course, based on both: judges base their decisions on firmly established precedent, but also map uncharted territory by bringing the full range of their experience to bear Knuth's "The Concept of a Meta-Font" , Visible Language, 16:4 (1982:Autumn) p.309 on specific cases “in a remarkably fluid way.” In this manner, the law itself adapts.
Hofstadter argues that an accordingly *spirited* conception of type design would therefore renounce Knuth’s ur-A-FORM in favor of a yet-higher- level abstraction, an ur-A-ESSENCE; the fundamental difference being that Hofstadter’s notion of “intelligence”extends beyond a Platonic shape, allowing for the concept of *what constitutes an A* to change, too — beyond what we can reasonably conceive of this possibly being in the future. Each new instance of an A adds to our general understanding of this idea (and ideal), which is necessarily assembled backwards over time.
Hofstadter includes this illustration of two letters vying for the same “typographic niche,” to make himself clear:

Continues in class ...
February 22, 2021
The polyhedron problem

Reading
Proofs-and-Refutations.pdf (Imre Lakatos)
Fluid-Geography.pdf (Buckminster Fuller)

Resources
https://www.bfi.org
Everything I Know (Buckminster Fuller)
1. A Problem and a Conjecture
The dialogue takes place in an imaginary classroom. The class gets interested in a PROBLEM: is there a relation between the number of vertices V, the number of edges E and the number of faces F of polyhedra — particularly of regular polyhedra — analogous to the trivial relation between the number of vertices and edges of polygons, namely, that there are as many edges as vertices: V = E ? This latter relation enables us to classify polygons according to the number of edges (or vertices): triangles, quadrangles, pentagons, etc. An analogous relation would help to classify polyhedra.
After much trial and error they notice that for all regular polyhedra V - E + F = 2. Somebody guesses that this may apply for any polyhedron whatsoever. Others try to falsify this conjecture, try to test it in many different ways — it holds good. The results corroborate the CONJECTURE, and suggest that it could be proved. It is at this point — after the stages *PROBLEM* and *CONJECTURE* — that we enter the classroom. The teacher is just going to offer a *proof.*

2. A Proof
TEACHER: In our last lesson we arrived at a conjecture concerning polyhedra, namely, that for all polyhedra V - E + F = 2, where V is the number of vertices, E the number of edges and F the number of faces. We tested it by various methods. But we haven’t yet proved it. Has anybody found a proof?
PUPIL SIGMA: ‘I for one have to admit that I have not yet been able to devise a strict proof of this theorem...As however the truth of it has been established in so many cases, there can be no doubt that it holds good for any solid. Thus the proposition seems to be satisfactorily demonstrated.” But if you have a proof, please do present it.
Sailor, inventor, teacher, dome-constructor, and 20th-century architect Buckminster Fuller offers proof in a more visual manner. His Dymaxion Maps offer a freshly bent image of the world departing from various unfoldings and projections of the sphere onto a series of polyhedra. The result is nothing short of a visual reconsideration of our world:

Continues in class ...
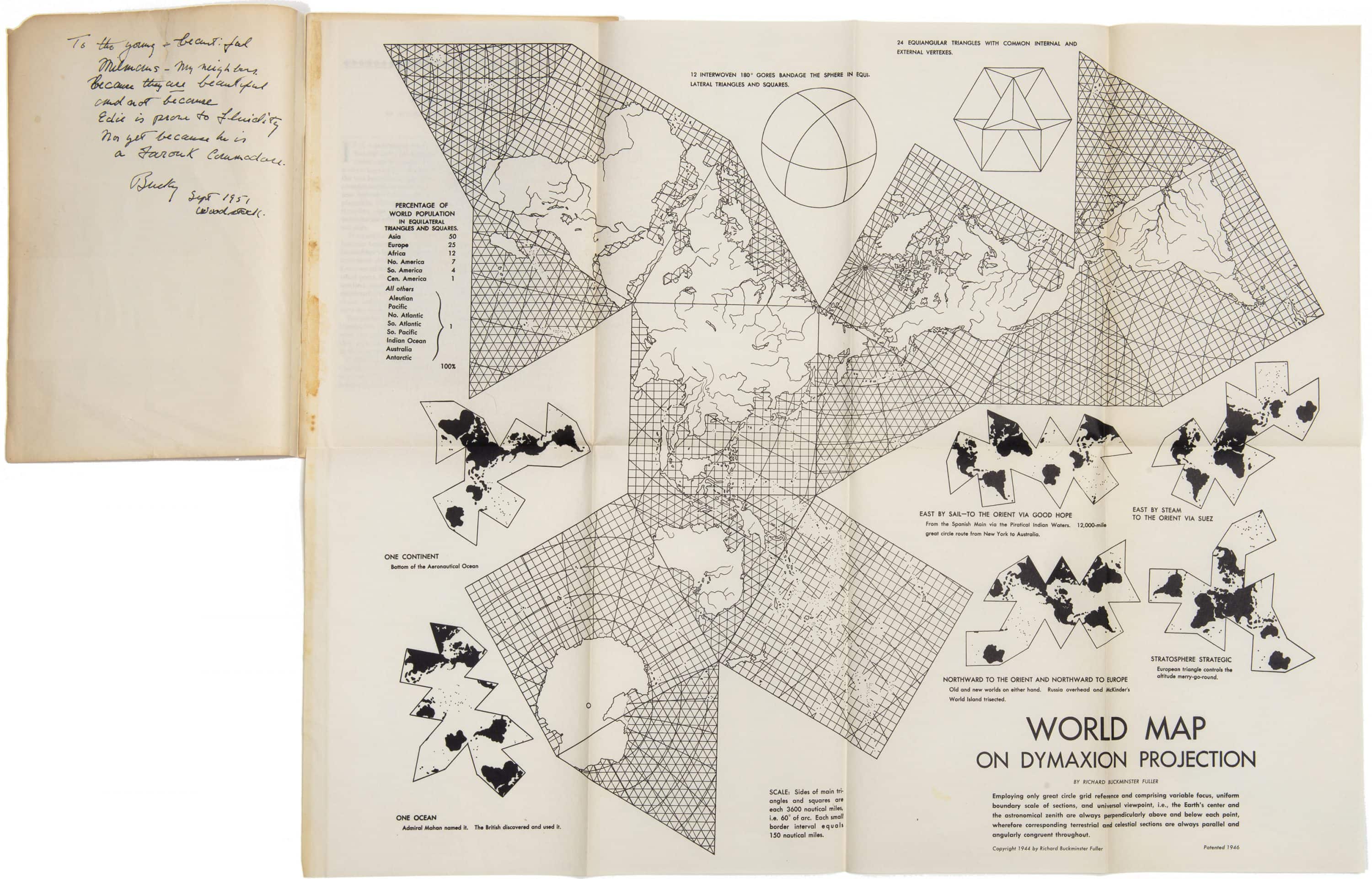
March 1, 2021
The inside out problem

Readings
Inside-Out.pdf (Steingart)

Resources
Department of History, Columbia University
grey room

Visitor
Alma Steingart, Department of History, Columbia University
The reason I was doing it was because I was trying to understand the geometry that’s implied by Steve’s theorem. Steve’s theorem is completely abstract and does not mention too much geometry in it. At least you can’t see the geometry. These models are an attempt to see what’s going on.
Sporting a crimson turtleneck, shoulder-length hair, and verdant beard, mathematician Charles Pugh gesticulates as he explains to physicist Judith Bergman what inspired him to spend hours of his free time constructing 1.6-foot chicken-wire models of a solution to a topological problem known as the sphere eversion: turning a sphere inside out.3 Both Pugh’s sartorial choices and the 16 mm film’s desaturated colors and tinny tones mark it as a product of the mid-1970s. Topological models hang from the ceiling behind Pugh, suspended from the walls of the newly opened Evans Hall, home to the department of mathematics at the University of California, Berkeley. Running the length of the wall, a succession of green, blue, and brown squares mounted behind the models ensures that the sculpted forms are clearly visible and do not recede into the wall behind them. Sitting on a computer chair to Pugh’s right, Stephen Smale (who proved the theorem in 1957) interjects into the conversation. The camera moves to the left as Smale smiles and adds, 
I take exception to you saying that my theory is completely abstract.
The two men laugh, as Pugh partially concedes, “yes, in principle, you can make geometric models from your theory. However,” he is quick to add, “no one was able to.”5 The friendly squabble is quickly left behind, as Pugh moves on to explain how he built his models.

In Smale and Pugh’s brief interaction, I detect two modes of mathematical engagement, which can broadly be described as an abstract and generalized approach on the one hand and a concrete and perceptual one on the other. One of the clearest examples of how mathematicians in the second half of the twentieth century have actively sought to merge the two and move beyond mere symbolic reasoning is the history of the sphere eversion, which has challenged mathematicians’ apprehension and perception for the past five decades. By following this story, I examine how these mathematicians traffic between the theoretical and the tangible, an idea and its instantiation, the abstract and the concrete.
The models Pugh displayed at Berkeley were neither the first nor the last solution mathematicians have devised to the sphere eversion problem. Like a classic novel adapted over and over again for screen and stage, during the past half-century mathematicians have constructed several solutions to the problem and have done so in multiple media. They have drawn the eversion on paper and modeled it in clay, chicken wire, plaster, fiberglass, and even ice. And they have programmed the eversion time and time again on computer screens.

Continues in class ...
March 8, 2021
The problem of continuity

Readings
Species-of-Spaces.pdf (Georges Perec)
Hypothesis.pdf (Adrian Piper)

Resources
Life-A-Users-Manual (Georges Perec)
Adrian Piper Foundation
The French novelist Georges Perec probably would have fared well during a pandemic. 

Besides the company of his cat, he enjoyed jigsaw puzzles. His book Life A User's Manual starts with a meditation on puzzles:
To begin with, the art of jigsaw puzzles seems of little substance, easily exhausted, wholly dealt with by a basic introduction to Gestalt: the perceived object – we may be dealing with a perceptual act, the acquisition of a skill, a physiological system, or, as in the present case, a wooden jigsaw puzzle – is not a sum of elements to be distinguished from each other and analysed discretely, but a pattern, that is to say a form, a structure: the element’s existence does not precede the existence of the whole, it comes neither before nor after it, for the parts do not determine the pattern, but the pattern determines the parts: knowledge of the pattern and of its laws, of the set and its structure, could not possibly be derived from discrete knowledge of the elements that compose it.
As you might perceive from this opening, jigsaw-like sentence, Perec finds, in fact, much of substance in puzzling.  A well designed puzzle anticipates the puzzler's "every blunder and every insight, each hope and each discouragement." Each piece inhabits the image to be reassembled in multiple and misleading ways.  
The problem of fitting things together depends on the relationships among the parts, and the number of potential relationships grows very quickly with the number of parts. One way to look for continuity is to focus on scale, as Perec does in his long essay Species of Spaces, written a few years before the User's Manual. Another way is to pursue paths as Adrian Piper did a few years earlier than Perec's Spaces in her artwork, The Hypothesis Series (1968-1970).  

Continues in class...
March 22, 2021
The knot problem

Reading
Mathematical-Games.pdf (Martin Gardner)

Resources
Braids and Knots (Joan Birman)
String Figures: The Collections of Harry Smith
One of the first metaphors for multiplicity in Calvino's lecture is the knot. Or, in the words of Gadda's Officer Ingravallo, "some gliuommero to untangle". A loop of string is flexible and easily formed in myriad ways, this way or that. 

But already in the amusement of string figures, there surfaces the potential of pattern within that multiplicity. Inoli Murphy found a way to put this potential to good use as a mathematics teacher. "Ancient String Patterns Sharpen Skills in Math" is how the New York Times reported it in an article that appeared in June, 1986. 

In learning to manipulate string into specific patterns, students "inadvertently learn systematic thinking," according to Keith Kaplon, another math teacher at La Guardia who learned about string figures from Mr. Murphy. 
Years later Murphy was curious whether math might return the favor to string figures. In particular, he asked if knot theory, a subfield of topology could prove his hunch that no portion of a string figure could ever contain a square knot or a granny knot.  

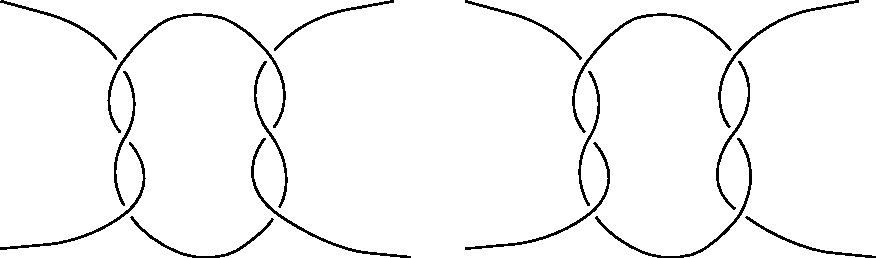
The question raises many more questions, not least among them being: what is a mathematical knot? Different knot diagrams give rise to different knot formalizations. The elementary arithmetic of braids is a good place to begin.  

Continues in class...
We are very fortunate to have artist Anthony McCall speaking with us this week. Here is a description in his own words of one of his most celebrated works. 
Line Describing a Cone is what I term a solid light film. It deals with the projected light beam itself, rather than treating the light beam as a mere carrier of coded information that is decoded when it strikes a flat surface.
The viewer watches the film by standing with his or her back towards what would normally be the screen, and looking along the beam towards the projector itself. The film begins as a coherent pencil of light, like a laser beam, and develops through 30 minutes into a complete, hollow cone.

Line Describing a Cone deals with one of the irreducible, necessary conditions of film: projected light. It deals with this phenomenon directly, independently of any other consideration. It is the first film to exist in real, three-dimensional space.
This film exists only in the present: the moment of projection. It refers to nothing beyond this real time. It contains no illusion. It is a primary experience, not secondary: that is, the space is real, not referential; the time is real, not referential.
No longer is one viewing position as good as any other. For this film, every viewing position presents a different aspect. The viewer therefore has a participatory role in apprehending the event: he or she can, indeed needs, to move around relative to the slowly emerging light form.
Continues in class...
April 5, 2021
The n-body problem

Readings
Round-and-Round-and-Round.pdf (Philip Ording)
The-Open-Work.pdf (Umberto Eco)

Resources
An important source of multiplicity is movement. Calvino writes
...what matters most is not the enclosure of the work within a harmonious figure, but the centrifugal force produced by it.
Taking a step away from the lectern, picture that force as choreographer Simone Forti described it:  
I found that if I stepped very quickly round and round a small circle I could lean very steeply in towards its apex. Almost strangely so. And it seemed that I could isolate nearly all the effort to my legs, and that I could abandon most of my weight to a waving flame-like energy that seemed to be rising up the center of the vortex .... I was developing an interest in drawing circles, and was training my hand to the proportions of the seven circles which form the basis of the Star of David and of the Arabic numerals. In my dancing I was banking from orbit to orbit.

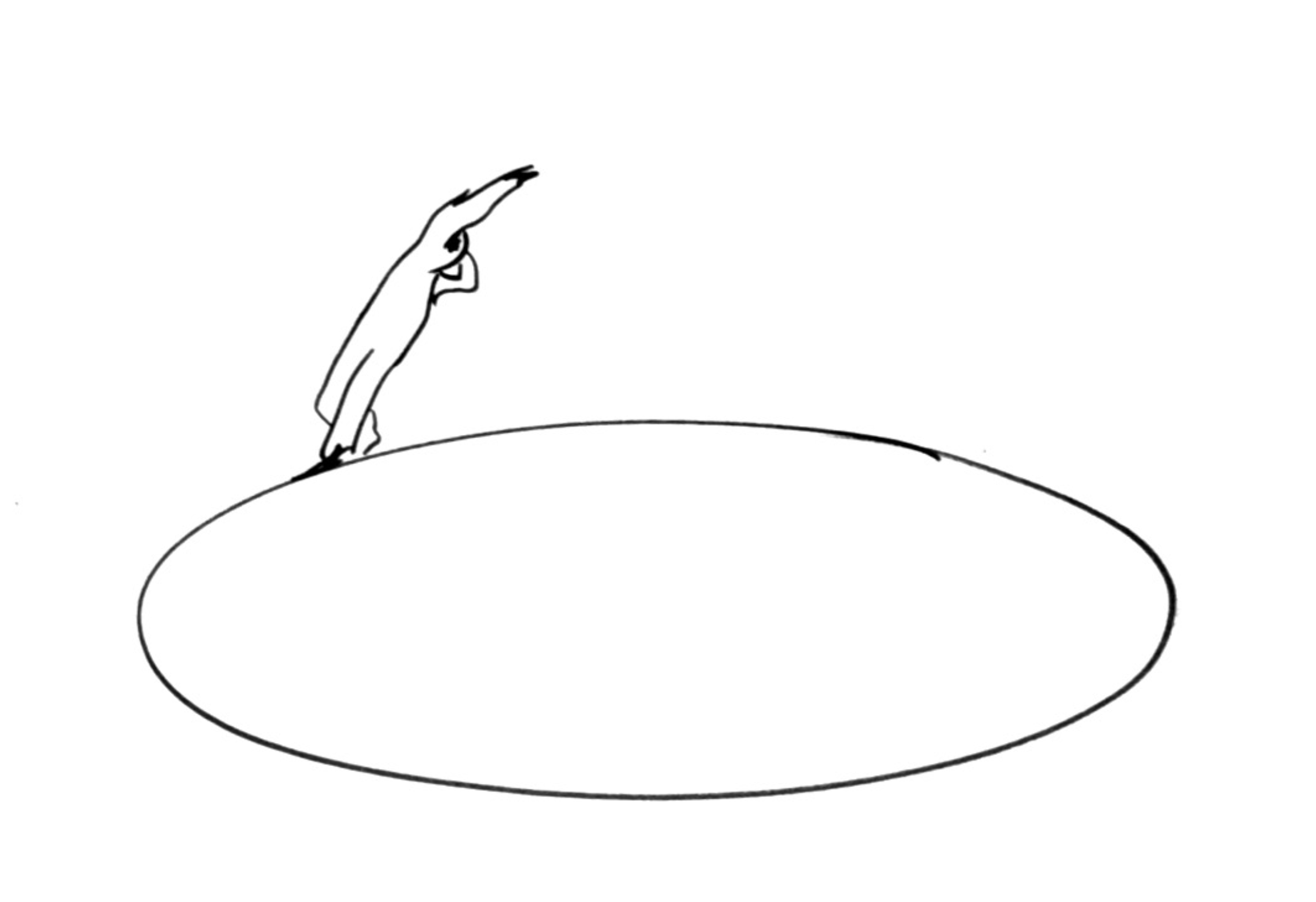
Forti attended technique classes with the most celebrated modern choreographers when she arrived in New York in 1959, but she was, by her own account, a lousy student. She wrote in her diary that she “couldn’t even perceive” what Martha Graham’s body was doing, let alone reproduce her movements. Merce Cunningham’s “adult, isolated articulation” was just as foreign. She had better luck the following year in a composition class offered at the Cunningham studio by musician Robert Dunn. He introduced her to compositional techniques of John Cage, who was the music director of Cunningham’s company. In a technique called Imperfections Overlay, Cage would trace any inconsistencies he found on the surface of a blank sheet of paper onto a transparency and then drop the transparency onto a grid. Once the “imperfections” were rationalized, they could be rendered, albeit imperfectly, as events in time and pitch. The scattered score could also become choreography.
In retrospect, I find that Imperfections Overlay, with its graph, was my first exposure to a still point of reference that gives a footing for a precise relationship to indeterminate systems. I had the feeling that the resultant piece would be a kind of ghost or trace of all the elements involved, including the original sheets of paper, and the air currents through which the plastic sheets had glided. It seemed to be a kind of notation whose interpretation by the performer would reawaken a partial presence of the original events.
This passage appears in Forti’s book Handbook in Motion: An Account of an Ongoing Personal Discourse and Its Manifestations in Dance. The book was my first exposure to a still point of reference for thinking about dance. Like Forti, I didn’t take a modern technique class until I was in my mid-20s, and I also found it perplexing. Less like Forti, I was at that time in dance class as a diversion from my graduate studies in mathematics. In Forti I find an understanding of movement that is at once enlightening, poetic, and often humorous. For example, she writes, “I saw a man in pajamas walk up to a tree, stop, regard it, and change his posture.”

In addition to an observational acuity, Forti reveals habits of mind that in an admittedly self-serving way I have long held to exhibit a mathematical attitude. Some of these analytic tendencies are evident in the passage quoted above — at least in her choice of the words “precise,” “indeterminate systems,” and “elements.” Mathematical clues appear elsewhere in the Handbook in the form of drawings of numerals and circles. And then there is her enigmatic “proposal: 1 = pi.” She has described her early work as “more closed systems than not, arrived at by abstracting and reordering elements of one situation to create another which is of a new order.” One of these early works is Huddle, perhaps her most widely performed piece.
Huddle requires six or seven people standing very close together, facing each other ... One person detaches and begins to climb up the out­ side of the huddle ... He pulls himself up, calmly moves across the top of the huddle, and down the other side. He remains closely identified with the mass, resuming a place in the huddle ... Immediately, someone else is climbing ... The duration should be adequate for the viewers to observe it, walk around it, get a feel of it in its behavior. Ten minutes is good.
She called this and the other works from the same period dance constructions because she “saw them as being somewhere between sculpture and dance.” These constructions, attained through abstracting and reordering elements bring to mind the geometric constructions of the Elements of Euclid.  

Umberto Eco, a contemporary and compatriot of Calvino, developed an aesthetic theory to account for works like Cage's and Forti's that are, by design, indeterminate. He called them open work:
They appeal to the initiative of the individual performer, and hence they offer themselves not as finite works which prescribe specific repetition along given structural coordinates but as "open" works, which are brought to their conclusion by the performer at the same times as he experiences them on an aesthetic plane.
...
The possibilities which the work's openness makes available always work within a given field of relations. 
Continues in class ...
April 12, 2021
The curve problem

Readings
Mathematical-Artefacts.pdf (Byron Cook)
When-X-is-Not-X.pdf (David Reinfurt)

Resources
https://www.taubaauerbach.com

Visitor
Tauba Auerbach
In 1890, Italian mathematician Giuseppe Peano described a particular curve which would fill completely the area of a square without touching it. This "space-filling curve" (since called a Peano Curve) is a mathematical absurdity. It’s a one-dimensional entity passing as a two-dimensional figure. I'd guess it is exactly this paradox that drew artist and designer Bruno Munari to the form starting in the late 1960s. Here is a set of drawings by Munari attempting to understand the form:

Munari called these specific algebraic-geometric constructions "pathological curves" and he began to explore them in his work. In December 1969 Munari made a print for La Rinascente department store in Milan called Arbitrary Variations on the Peano Curve. I expect “Arbitrary” is the key word here. Soon he started making paintings and prints based on Peano curves where he indulged his instinct to oppose the “scientific nature” of the mathematical forms with an irrational component:
My proposal, absolutely superfluous to mathematical speculation, but curious from an aesthetic point of view, is to place certain colors in the areas delimited by the line
Munari continues:
I wanted to try to insert in this very rigorous, mathematical structure an emotional fact based instead on the sensitivity of color. I asked myself: what happens if I insert a fact of chromatic sensitivity into a strictly logical problem? The truth that color finds its own structure even if it has an emotional origin because Peano can explain its structure with logic while I cannot explain in words what sensitivity is. So it is a relationship between sensitivity, intuition and logic.
He made a set of prints for Danese Milano based on the images. These are his color studies which give some slight insight to the process.

And here is a finished picture. I love these so much.

In the catalog from a 2017 exhibition of Munari’s work, Giuseppe Virelli writes:
... like many other of his works, the Munari curves can also be considered "open works," as they require the active participation of the viewer, that is, they open up to a relational dimension. And Munari himself, moreover, clarifies the terms of this participatory vision, specifying that the user must first interact with the work and, above all, “complete it” with his own imagination: 
“Faced with this proposal, the observer is forced to imagine what the color of the square surface could be when the curve, shrinking and multiplying, has filled it almost entirely. You don't need to think about it all the time, just once in a while.”
Other artists have picked up the curve since. One is Tauba Auerbach, an artist, designer, publisher and Im-not-sure-what-else based in New York. In 2020, they designed and released these pins based on Peano:

We are lucky to have Tauba joining us in class today. So I will stop for now.
Continues in class ...
April 19, 2021
The problem of structure

Reading
Bourbaki.pdf (Maurice Mashaal)

Resources
Sculpture-in-the-Expanded-Field.pdf (Rosalind Krauss)
"Irrational Thoughts Should be Followed Absolutely and Logically" (Mariabruna Fabrizi)
http://adampendleton.net
Among mathematicians, the one who embodies the quality of multiplicity most forcefully is Nicolas Bourbaki. Bourbaki is encyclopedic: the Éléments de mathématique is a basis for the entire discipline, it is the modern Euclid. Bourbaki is unified: all mathematics is structure, in fact, there is no need for an ’s’ at the end of mathématique. What is structure? Bourbaki's 1948 manifesto, “The Architecture of Mathematics” explains: 
The organizing principle will be the concept of a hierarchy of structures, going from the simple to the complex, from the general to the particular. At the center of our universe are found the great types of structures...they might be called the mother-structures.
Not only do all mathematical objects relate to each other in a grand abstract formalism, but each individual mathematical object exists according to the relationships among its internal component parts. This is the nature of structure:
The common character of the different concepts designated by this generic name [structure], is that they can be applied to sets of elements whose nature has not been specified; to define a structure, one takes as given one or several relations, into which these elements enter... then one postulates that the given relation, or relations, satisfy certain conditions...
True to its principles, Bourbaki itself is a structure. A secret (more or less) set of ambitious, young, mostly French mathematicians adopted the nom de plume of Nicolas Bourbaki for their radical project to rewrite mathematics. A 1937 conference in central France shows founding members André Weil, Henri Cartan, Szolem Mandelbrojt, and Claude Chevalley (Simone Weil, André's sister and Bourbaki confidant, stands above).

The structuralist passion of the 20th century extended from math into linguistics, psychology, literature, music, and art. A famous example in art history is Rosalind Krauss' use of the Klein group in "Sculpture in the Expanded Field" to situate new forms of sculpture in relation to landscape and architecture and their opposites.
The expanded field is thus generated by problematizing the set of oppositions between which the modernist category sculpture is suspended. And once this has happened, once one is able to think one's way into this expansion, there are — logically — three other categories that one can envision, all of them a condition of the field itself, and none of them assimilable to sculpture. Because as we can see, sculpture is no longer the privileged middle term between two things that it isn't. Sculpture is rather only one term on the periphery of a field in which there are other, differently structured possibilities. And one has thereby gained the "permission" to think these other forms. So our diagram is filled in as follows: 

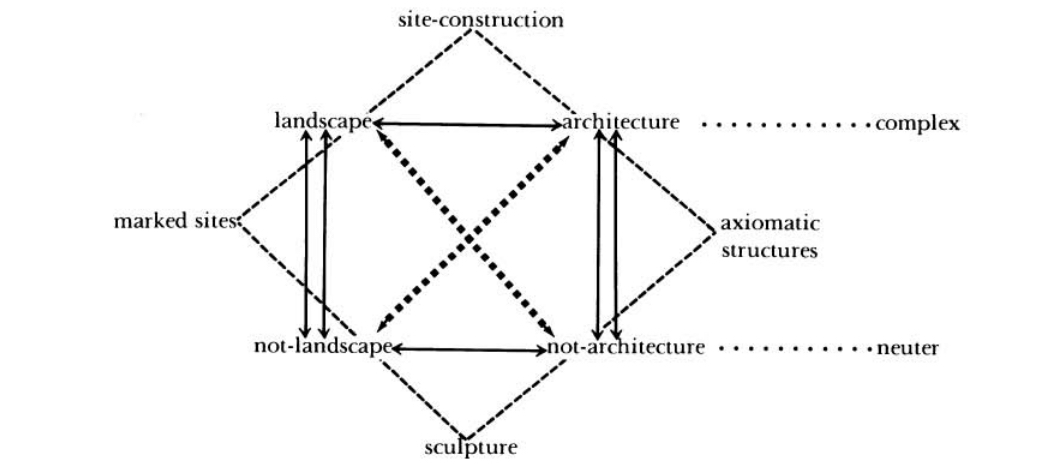
Notice that there is a part of the above schema that mirrors itself: "axiomatic structures". As an example of this mise en abime of architecture/not-architecture, she cites (among others) the work of Sol LeWitt. 

Continues in class...
You’ll recall from Week 1 (The bridges problem), Ralph Caplan describing The Eames Office's work with M.I.T.:
And the payoff is a connection. No arbitrary reward for good behavior, it is tied inextricably to the experience that generates it. This is why, when consulted by a Massachusetts Institute of Technology as to the best way to infuse their technologically heavy curriculum with art, the Eames rejected the idea of additional art courses or fine arts programs as “an aesthetic vitamin concentrate.” Instead they designed an alternative situation, a program for enriching the student‘s (and the university’s) communicative capabilities to the point where they could experience the aesthetic possibilities of their own discipline.

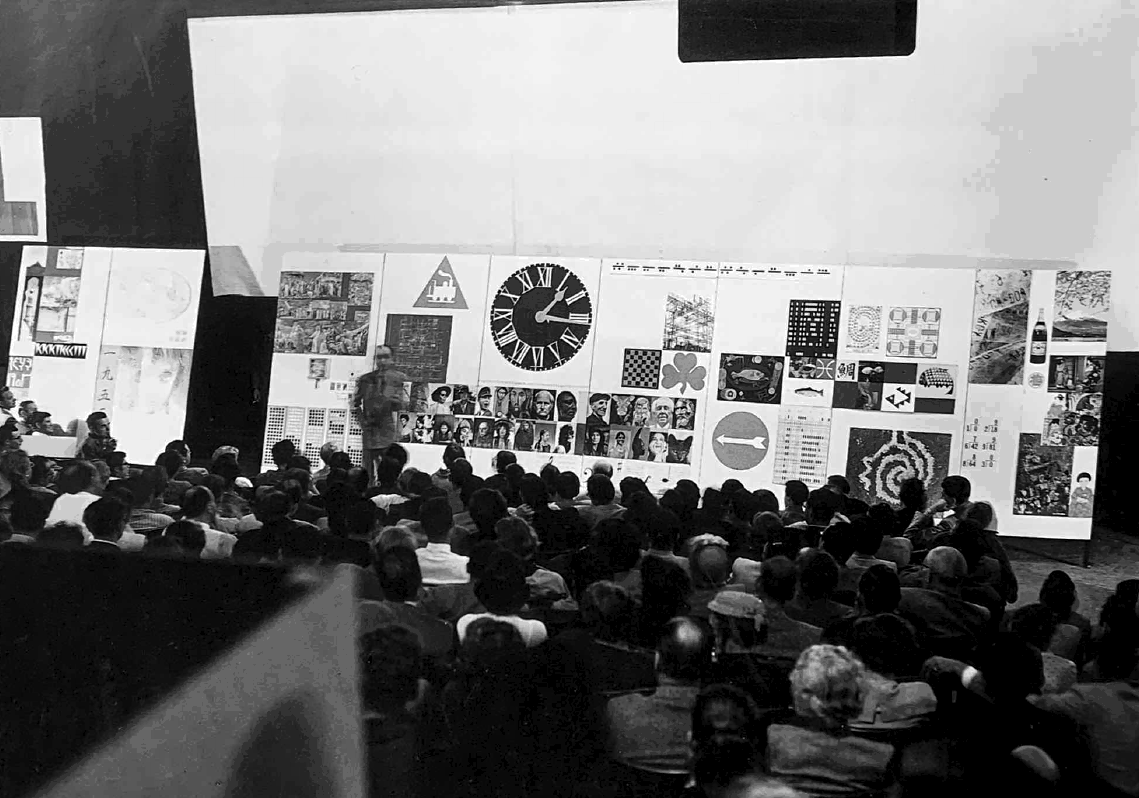
The situation they designed had two essential parts. The first called for each academic department to include a unit of teaching assistants whose first allegiance was to the departmental discipline but who also were gifted and trained in film, graphics, and writing. Their responsibility was to produce packets of current information that would keep everyone within the department aware of what was going on. The best of the packets would be made available outside the department, and the best of those would be distributed outside the university. Work done by these units was to be “insight motivated, arriving at as well as conveying insight)” thus precluding the creation of still another campus media center to prepare slides on demand from instructors who wished to beef up non-visual material. Not that no technical service center would be needed; clearly one would. But it would be designed to service the twenty-five or so professional units.
The beauty of the scheme is that it allows for the introduction of aesthetics as required for pleasure and communication, not just as another base to be touched before a student is home safe.
The second part would involve each student; for each, near the end of their M.I.T. career, would join one or two other students in teaching something of their major specialty to an elementary school class for a semester. The teaching could take the form of films, exhibits, lectures, games, models — whatever the team needed to make what they knew and understood meaningful to children. “...If the M.I.T. student is going to learn anything about art,” Eames argued, “they will learn it here.”
The entire design repudiates conventional approaches to the same goal. These mainly consist of three kinds of programs. One gives students massive doses of high art (no one gets a diploma without taking “appreciation” courses to guarantee that he has heard, if not listened to, Beethoven’s Ninth Symphony and looked at, if not seen, a Dutch Master or a reproduction of one). Another is an egalitarian attempt to “reach the student where they are” by running them through courses in rock and roll, horror movies, great graffiti of the sixties, etc. A third is the studio approach of encouraging the student to “do it themself” on the grounds that their “it” is as aesthetically valid as anyone else's. (It may be, but it is not as aesthetically rewarding.) The Eames design calls for appreciation through the experience of searching out the aesthetic character of the student’s own discipline. It also includes another favorite Eames idea: the university as a found object, a collection of traditions and facilities already on hand that can be transformed by fresh perception.
So then, your final project in five steps:
1. Ask yourself a question which has many equally correct answers. *
2. Answer the question by discovering and populating the multiplicity of valid responses. ** 
3. Organize your solutions. ***
4. Your result should be a well-formulated problem together with a multiplicity of possible answers. ****
5. Now, teach us (the class) your problem and its many answers. *****
* The problem can be anything but should be specific to your discipline. Philip also notes, “When I ask myself a question I don't usually know or worry about multiple, equally correct answers. I just aim for interesting questions and explore the space of variations along the way.”
** Consider the topological approaches we've studied: schematic diagramming, constructing a manifold in one or more dimensions, interpolating solutions, deforming solutions, flattening them out, etc.
*** It may be useful to refer to the three models of multiplicity that Italo Calvino offered: “as an encyclopedia, as a method of knowledge, and above all as a network of connections.” For more, see https://m-u-l-t-i-p-l-i-c-i-t-y.org/media/pdf/Multiplicity.pdf
**** For more on manifolds and multiplicities, see https://m-u-l-t-i-p-l-i-c-i-t-y.org/february-8
***** You will present your problem and project in the final class in April 26. See https://m-u-l-t-i-p-l-i-c-i-t-y.org/april-26
loading...