One of the first metaphors for multiplicity in Calvino's lecture is the knot. Or, in the words of Gadda's Officer Ingravallo, "some gliuommero to untangle". A loop of string is flexible and easily formed in myriad ways, this way or that.

But already in the amusement of string figures, there surfaces the potential of pattern within that multiplicity. Inoli Murphy found a way to put this potential to good use as a mathematics teacher. "Ancient String Patterns Sharpen Skills in Math" is how the New York Times reported it in an article that appeared in June, 1986.

In learning to manipulate string into specific patterns, students "inadvertently learn systematic thinking," according to Keith Kaplon, another math teacher at La Guardia who learned about string figures from Mr. Murphy.
Years later Murphy was curious whether math might return the favor to string figures. In particular, he asked if knot theory, a subfield of topology could prove his hunch that no portion of a string figure could ever contain a square knot or a granny knot.
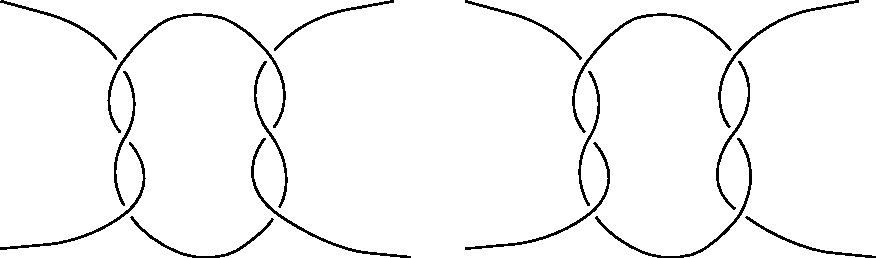
The question raises many more questions, not least among them being: what is a mathematical knot? Different knot diagrams give rise to different knot formalizations. The elementary arithmetic of braids is a good place to begin.

March 22, 2021
The knot problem
Reading
The knot problem
Reading
Mathematical-Games.pdf (Martin Gardner)
Resources
Braids and Knots (Joan Birman)