1. A Problem and a Conjecture
The dialogue takes place in an imaginary classroom. The class gets interested in a PROBLEM: is there a relation between the number of vertices V, the number of edges E and the number of faces F of polyhedra — particularly of regular polyhedra — analogous to the trivial relation between the number of vertices and edges of polygons, namely, that there are as many edges as vertices: V = E ? This latter relation enables us to classify polygons according to the number of edges (or vertices): triangles, quadrangles, pentagons, etc. An analogous relation would help to classify polyhedra.
After much trial and error they notice that for all regular polyhedra V - E + F = 2. Somebody guesses that this may apply for any polyhedron whatsoever. Others try to falsify this conjecture, try to test it in many different ways — it holds good. The results corroborate the CONJECTURE, and suggest that it could be proved. It is at this point — after the stages *PROBLEM* and *CONJECTURE* — that we enter the classroom. The teacher is just going to offer a *proof.*

2. A Proof
TEACHER: In our last lesson we arrived at a conjecture concerning polyhedra, namely, that for all polyhedra V - E + F = 2, where V is the number of vertices, E the number of edges and F the number of faces. We tested it by various methods. But we haven’t yet proved it. Has anybody found a proof?
PUPIL SIGMA: ‘I for one have to admit that I have not yet been able to devise a strict proof of this theorem...As however the truth of it has been established in so many cases, there can be no doubt that it holds good for any solid. Thus the proposition seems to be satisfactorily demonstrated.” But if you have a proof, please do present it.
Sailor, inventor, teacher, dome-constructor, and 20th-century architect Buckminster Fuller offers proof in a more visual manner. His Dymaxion Maps offer a freshly bent image of the world departing from various unfoldings and projections of the sphere onto a series of polyhedra. The result is nothing short of a visual reconsideration of our world:
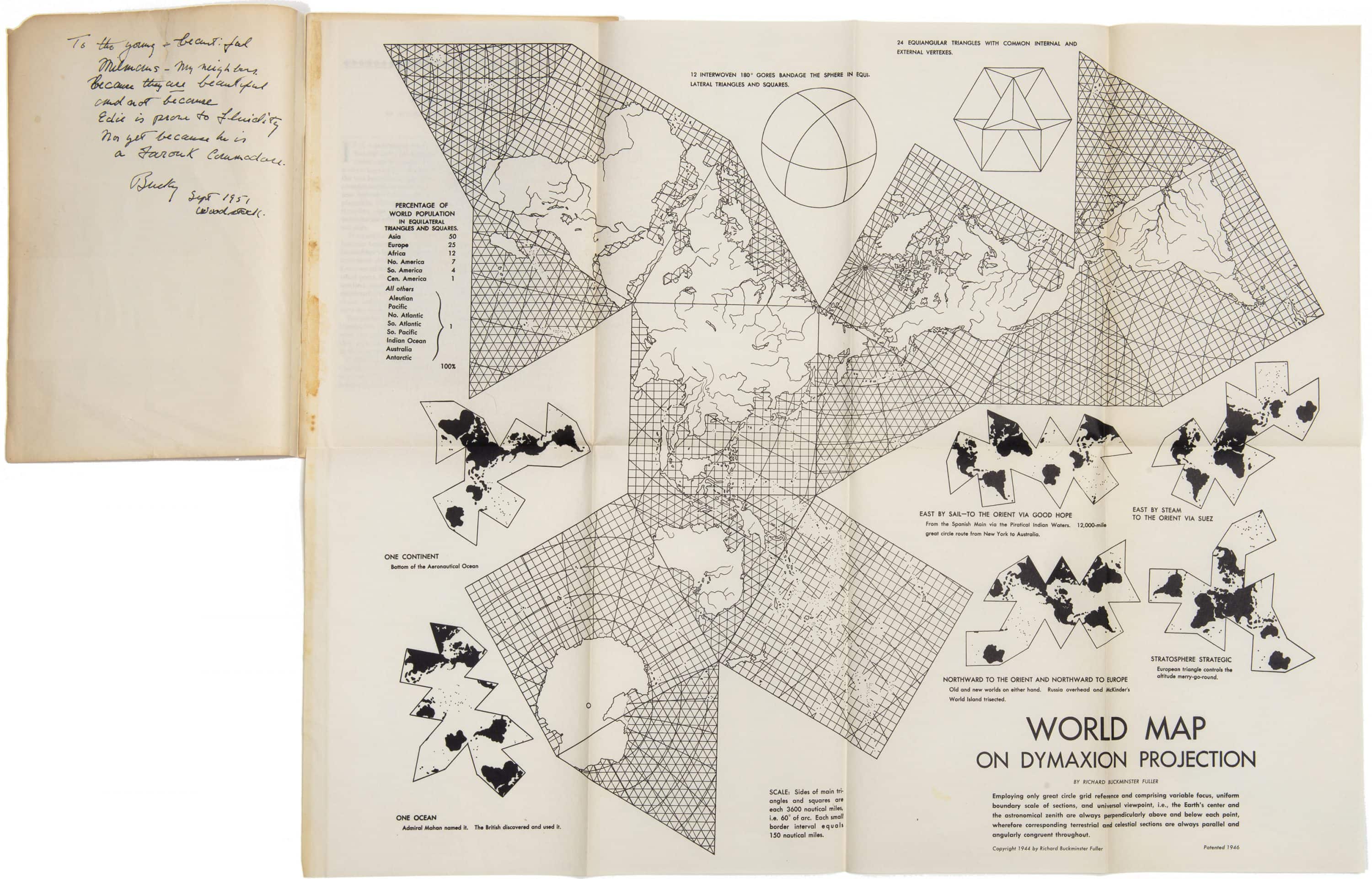
February 22, 2021
The polyhedron problem
The polyhedron problem
Reading
Proofs-and-Refutations.pdf (Imre Lakatos)
Everything I Know (Buckminster Fuller)