Among mathematicians, the one who embodies the quality of multiplicity most forcefully is Nicolas Bourbaki. Bourbaki is encyclopedic: the Éléments de mathématique is a basis for the entire discipline, it is the modern Euclid. Bourbaki is unified: all mathematics is structure, in fact, there is no need for an ’s’ at the end of mathématique. What is structure? Bourbaki's 1948 manifesto, “The Architecture of Mathematics” explains:
The organizing principle will be the concept of a hierarchy of structures, going from the simple to the complex, from the general to the particular. At the center of our universe are found the great types of structures...they might be called the mother-structures.
Not only do all mathematical objects relate to each other in a grand abstract formalism, but each individual mathematical object exists according to the relationships among its internal component parts. This is the nature of structure:
The common character of the different concepts designated by this generic name [structure], is that they can be applied to sets of elements whose nature has not been specified; to define a structure, one takes as given one or several relations, into which these elements enter... then one postulates that the given relation, or relations, satisfy certain conditions...
True to its principles, Bourbaki itself is a structure. A secret (more or less) set of ambitious, young, mostly French mathematicians adopted the nom de plume of Nicolas Bourbaki for their radical project to rewrite mathematics. A 1937 conference in central France shows founding members André Weil, Henri Cartan, Szolem Mandelbrojt, and Claude Chevalley (Simone Weil, André's sister and Bourbaki confidant, stands above).

The structuralist passion of the 20th century extended from math into linguistics, psychology, literature, music, and art. A famous example in art history is Rosalind Krauss' use of the Klein group in "Sculpture in the Expanded Field" to situate new forms of sculpture in relation to landscape and architecture and their opposites.
The expanded field is thus generated by problematizing the set of oppositions between which the modernist category sculpture is suspended. And once this has happened, once one is able to think one's way into this expansion, there are — logically — three other categories that one can envision, all of them a condition of the field itself, and none of them assimilable to sculpture. Because as we can see, sculpture is no longer the privileged middle term between two things that it isn't. Sculpture is rather only one term on the periphery of a field in which there are other, differently structured possibilities. And one has thereby gained the "permission" to think these other forms. So our diagram is filled in as follows:
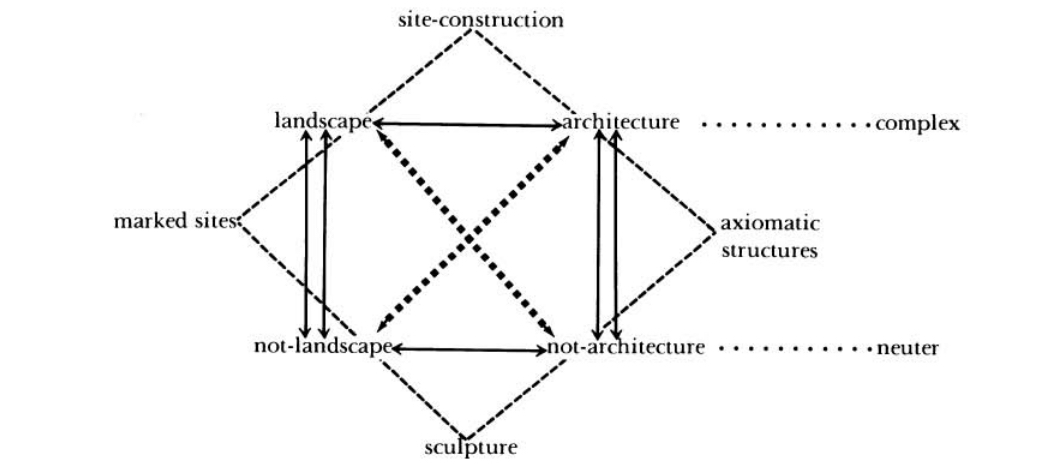
Notice that there is a part of the above schema that mirrors itself: "axiomatic structures". As an example of this mise en abime of architecture/not-architecture, she cites (among others) the work of Sol LeWitt.

April 19, 2021
The problem of structure
Reading
The problem of structure
Reading
Bourbaki.pdf (Maurice Mashaal)
Resources
Sculpture-in-the-Expanded-Field.pdf (Rosalind Krauss)
"Irrational Thoughts Should be Followed Absolutely and Logically" (Mariabruna Fabrizi)