1. THE branch of geometry that deals with magnitudes has been zealously studied throughout the past, but there is another branch that has been almost unknown up to now; Leibnitz spoke of it first, calling it the “geometry of position” (geometria situs). This branch of geometry deals with relations dependent on position alone, and investigates the properties of position; it does not take magnitudes into consideration, nor does it involve calculation with quantities. But as yet no satisfactory definition has been given of the problems that belong to this geometry of position or of the method to be used in solving them. Recently there was announced a problem that, while it certainly seemed to belong to geometry, was nevertheless so designed that it did not call for the determination of a magnitude, nor could it be solved by quantitative calculation; consequently I did not hesitate to assign it to the geometry of position, especially since the solution required only the consideration of position, calculation being of no use. In this paper I shall give an account of the method that I discovered for solving this type of problem, which may serve as an example of the geometry of position.

225 years later, designers Ray and Charles Eames unpacked this "geometry of connections," or topology, in their first exhibition designed and produced to inaugurate the California Museum of Science and Industry. “Mathematica” was an exhibition about mathematics for a mass and diverse audience. It was originated by the Eames Office following an invitation to propose an appropriate exhibition for the new museum. 

Yes. The whole purpose of that show was "Lifting the corner of the tent" to let people know the pleasure and the joy that mathematicians had in their work. So when you see the workings of any of those things — the soap bubble — it reflects the terrific joy that was originally felt in the discovery of that model, or in the use of models, the use of thinking, and the result of observation and relationships in observation, and relationships of knowing what someone did and someone didn't do. The chart shows how different people were influenced by different things, things happening because of other things, as a result of other things happening, things in the past happening, things coming together at the right time — all those layers of happenings. 

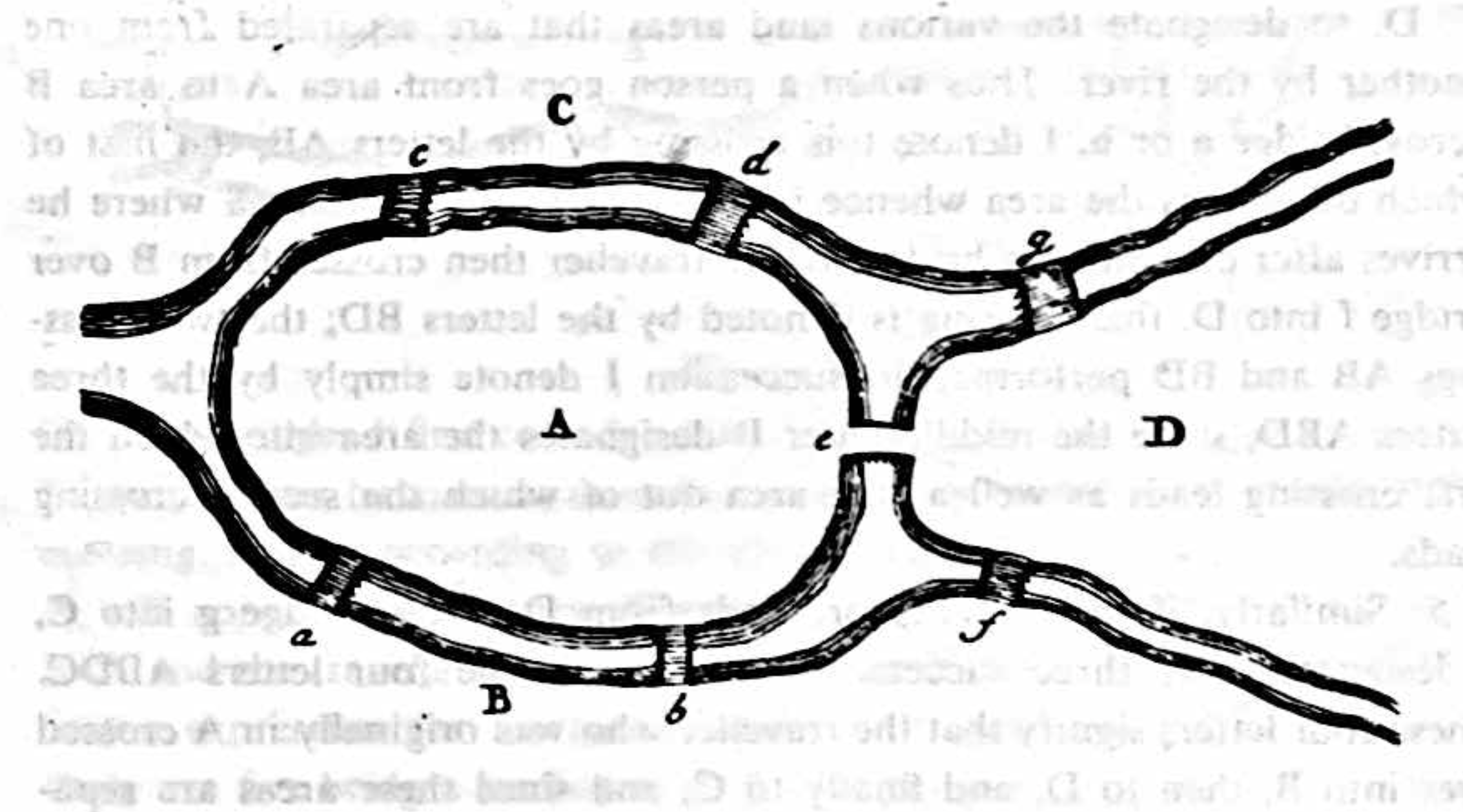
2. The problem, which I understand is quite well known, is stated as follows: In the town of Königsberg in Prussia there is an island A, called “Kneiphof,” with the two branches of the river (Pregel) flowing around it, as shown in Figure 1. There are seven bridges, a, b, c, d, e, f and g, crossing the two branches. The question is whether a person can plan a walk in such a way that he will cross each of these bridges once but not more than once. I was told that while some denied the possibility of doing this and others were in doubt, there were none who maintained that it was actually possible. On the basis of the above I formulated the following very general problem for myself: Given any configuration of the river and the branches into which it may divide, as well as any number of bridges, to determine whether or not it is possible to cross each bridge exactly once.

Eventually everything connects — people, ideas, objects ... the quality of the connections is the key to quality per se.