“Most of what science orders,” Phylis and Philip Morrison remind us, “was once unknown and was newly grasped while it remained in a more or less extended period of doubt and uncertainty.” The geometry of position remained in such a period of novelty for at least a century after Euler solved the bridges problem. Topology in the mid 1800s was a collection of examples and counterexamples at the periphery of mathematics. A decisive step forward was made by the German mathematician Bernhard Riemann in his 1854 lecture "On the Hypotheses Which Lie at the Foundations of Geometry" in which he outlined the notion of a topological manifold. He begins by noting that:
few and far between are the occasions for forming notions whose specialisations make up a continuous manifoldness, that the only simple notions whose specialisations form a multiply extended manifoldness are the positions of perceived objects and colours.
The awkward language of “specialisations” and “manifoldness” is due in part to the avant garde nature of Riemann’s project. He wants to identify spatial features that are pre-geometric, which means that familiar spatial terms of magnitude and measure are prohibited. Euler confronted the same issue. But unlike the 1-dimensional bridges of Königsberg, the problem Riemann set himself was to construct a metaspace with 1, 2, 3, or any number of dimensions. Riemann proceeds step by step: For a 1-dimensional manifold,
the true character is that in it a continuous progress from a point is possible only on two sides, forwards or backwards.
He mentioned color already, to which we can add the spectrum of sound. Consider for example the bow position as you listen to songs for the tape-bow violin by Laurie Anderson.

On to the next dimension... Riemann continues:
If one now supposes that this manifoldness in its turn passes over into another entirely different, and again in a definite way, namely so that each point passes over into a definite point of the other, then all the specialisations so obtained form a doubly extended manifoldness.
To get past the linguistic hurdles of this passage, let's extend the musical analogy. Think of a 1-manifold as a tune that begins on a particular note. A slightly different tune will result if it is shifted up or down in pitch. The space formed by transposing the tune arbitrarily in pitch forms a 2-manifold. Two dimensions of music are especially visible in a player piano scroll like the one below, Study for Piano Player No. 36 by Conlon Nancarrow.
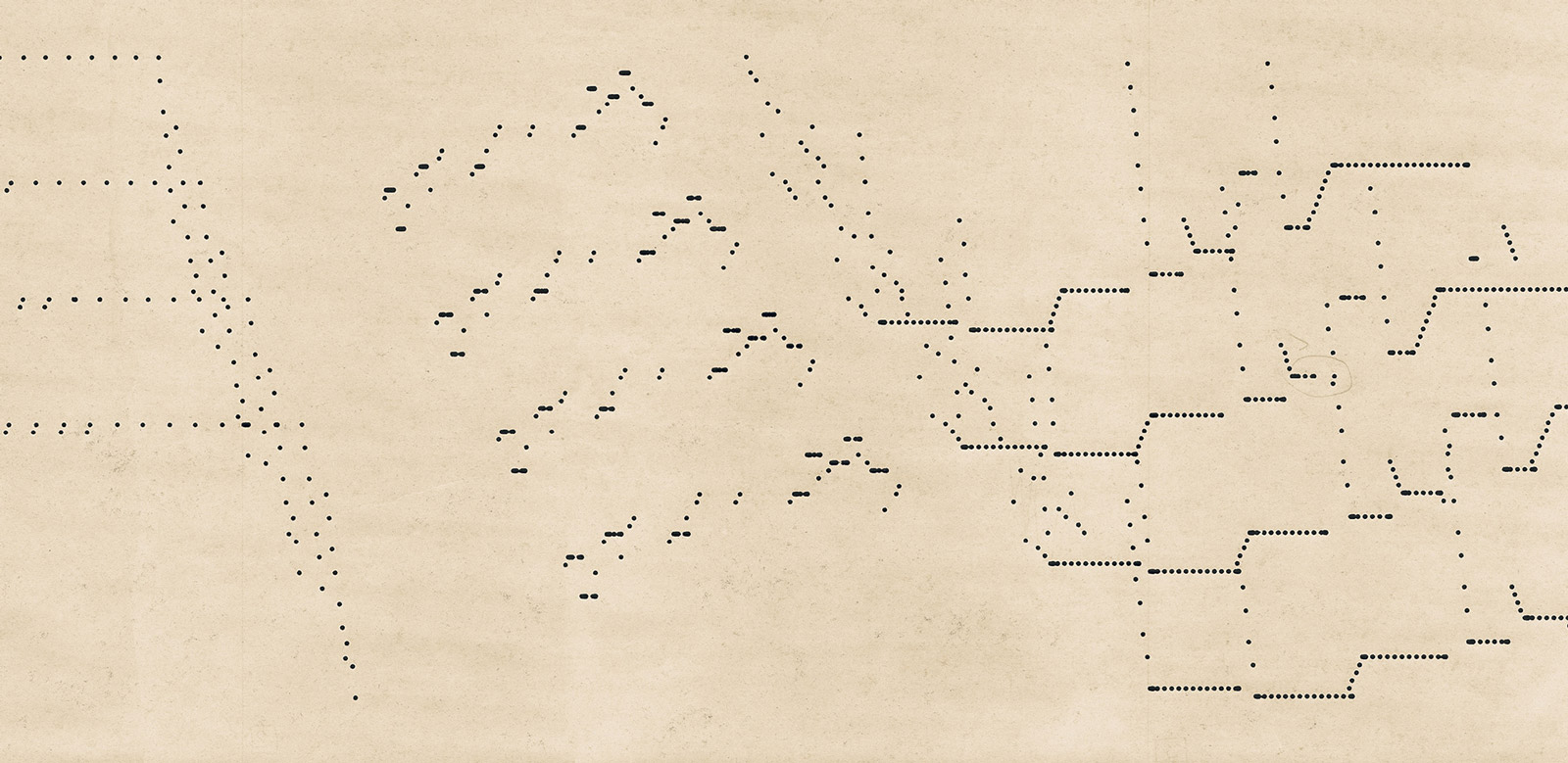
The 3- and higher-dimensional manifolds are constructed by analogy:
In a similar manner one obtains a triply extended manifoldness, if one imagines a doubly extended one passing over in a definite way to another entirely different; and it is easy to see how this construction may be continued.
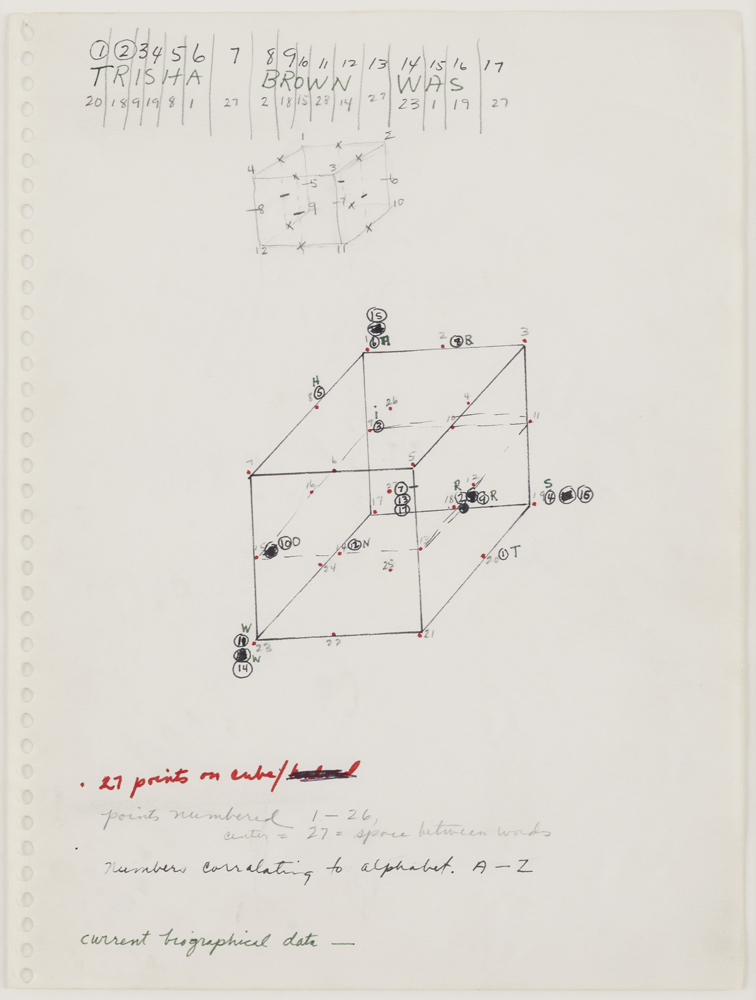
These manifolds are more difficult to visualize than 1-manifolds (curves) and 2-manifolds (surfaces). For an example of a discrete 3-manifold, watch Locus Solo, the dance Trisha Brown devised from a cubical framework. Each of 26 points on the surface of the cube corresponds to a different letter of the alphabet. In a reversal of Euler’s method, the series of letters in a given text dictate the dancer’s path.
Before giving the above construction, Riemann apologized to his audience for not being “practised in such undertakings of a philosophical nature where the difficulty lies more in the notions themselves than in the construction.” Rather than attempt such an undertaking ourselves here, we wish to lean on the philosophico-literary observations of Six Memos for the Next Millenium by Italian writer Italo Calvino. The memos are lectures he was invited to give as Charles Eliot Norton Professor of Poetry at Harvard University. Each lecture is organized around a one-word literary value. The fifth lecture Calvino drafted was on "Multiplicity." About three quarters of the way through, Calvino gets down to business:
It is time to put a little order into the suggestions I have put forward as examples of multiplicity. There is such a thing as the unified text that is written as the expression of a single voice, but that reveals itself as open to interpretation on several levels. Here the prize for an inventive tour-de-force goes to Alfred Jarry for L'amour absolu (1899), a fifty-page novel that can be read as three completely different stories: (1) the vigil of a condemned man in his cell the night before his execution; (2) the monologue of a man suffering from insomnia, who when half asleep dreams that he has been condemned to death; (3) the story of Christ. Then there is the manifold text, which replaces the oneness of a thinking “I” with a multiplicity of subjects, voices, and views of the world, on the model of what Mikhail Bakhtin has called “dialogic” or “polyphonic” or “carnivalesque,” tracing its antecedents from Plato through Rabelais to Dostoevsky. There is the type of work that, in the attempt to contain everything possible, does not manage to take on a form, to create outlines for itself, and so remains incomplete by its very nature, as we saw in the cases of Gadda and Musil.
As a short example of the last type, he cites "The Garden of Forking Paths," one of the short stories in the collection Labyrinths by the Argentine poet, essayist, and author Jorge Luis Borges.

Calvino picks the thought back up several pages later:
I have come to the end of this apologia for the novel as a vast net. Someone might object that the more the work tends toward the multiplication of possibilities, the further it departs from that unicum which is the self of the writer, his inner sincerity and the discovery of his own truth. But I would answer: Who are we, who is each one of us, if not a combinatoria of experiences, information, books we have read, things imagined? Each life is an encyclopedia, a library, an inventory of objects, a series of styles, and everything can be constantly shuffled and reordered in every way conceivable.
But perhaps the answer that stands closest to my heart is something else: Think what it would be to have a work conceived from outside the self; a work that would let us escape the limited perspective of the individual ego, not only to enter into selves like our own but to give speech to that which has no language, to the bird perching on the edge of the gutter, to the tree in spring and the tree in fall, to stone, to cement, to plastic. . . . .
Was this not perhaps what Ovid was aiming at, when he wrote about the continuity of forms? And what Lucretius was aiming at when he identified himself with that nature common to each and every thing?
February 8, 2021
The problem of multiplicity
Readings
The problem of multiplicity
Readings
Multiplicity.pdf (Italo Calvino)
The-Garden-of-Forking-Paths.pdf (Jorge Luis Borges)
Resources
Songs for the tape bow violin (Laurie Anderson)
Study for Player Piano No. 36 (Conlon Nancarrow)
Locus Solo (Trisha Brown)